这几道古代数学题，文科生都会做，理科生看完想打人

今天早上出了条新闻：考古学家在河南省“许昌人”遗址出土的一个小骨片上发现了经红赭石涂染的7条平行刻划直线。这件人工制品距今11万年左右，比来自南非的***古老现代人的画作早约4万年，可能是已知***早的人工刻划作品。

有专家解读说，这份骨片上的横线，可能是古代人的绘画或数学计算的痕迹。

我们都知道，古人一早就学会了结绳记事。划横线其实和结绳记事是一个道理，我们可以大胆想象一下：

***傍晚，部落里的会计站在村口统计今日族人们的狩猎成果。***个归来，带回来一只兔子，划一横；第二个人归来，带回来一只野猪，划一横……如此一来，就可以大致估摸当晚轰趴食物是否够吃。

在外国人的印象中，中国人的口算、心算能力要比他们高不止三个档次，或许，从老祖宗结绳记事、划横线记事这事儿开始，就已经奠定了血液中原始的数学基因。

今天，咱们就来看看古代那些强大的数学计算能手和数学题。

一

商高是我国古代***位数学家，生于大约公元前十一世纪。历史上很少记录关于他的生平，大概只知道他和周公是同一时期的人。

商高

在《周髀算经》中罕见地记载了一则“周公问数”的典故：

有***，周公对伏羲构造周天历度的事迹感到惊叹，便虚心求教商高：“我听说先生非常擅长数学，那么请教先生，这天地之间的距离怎么计算？”

商高思考了片刻，便回答说：“故折矩，以为勾广三，股修四，径隅五”。

商高这段话，简单点说就是：“数是根据圆和方的计算得来的，圆来自于方，方来自于直角三角形。当一条直角边（勾）为3，另一条直角边（股）为4，则斜边（弦）为5。”

后人根据其特性，将之命名为“勾三股四弦五”，简称“勾股定理”也叫“商高定理”。

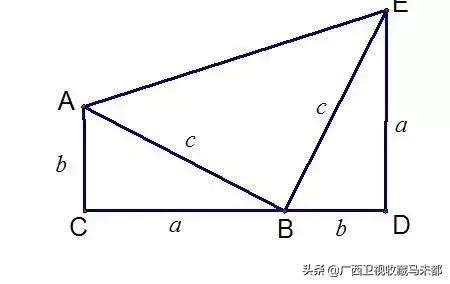
以商高命名的勾股定理，不仅是中华民族的骄傲，还确定了东方几何学开创的“原点”，是几何学中一颗光彩夺目的明珠，被称为“几何学的基石”。

而在遥远的西方，600年之后毕达哥拉斯（Pythagoras）才出生，不过由于毕达哥拉斯***早对此进行了证明，所以后人将其归功于毕达哥拉斯。

唉，商高君，当年你怎么能忘了写证明呢？

二

今有雉兔同笼，

上有三十五头，

下有九十四足，

问雉兔各几何？

——《孙子算经》卷下第31题

【译文】今有鸡兔关在一个笼子里，上有头35个，下有足94只。问鸡兔各多少？

注：“鸡兔同笼”问题的模型是：“已知鸡兔头数与脚数，求鸡兔各几？”解法也多，如以兔脚为主元或以鸡脚为主元，采用算术方法或代数法等。

【解法】（算术解法之一）以兔脚为主元思考：

设想头35全是兔，则应有35×4=140只脚，这样多出了46只脚，可以用兔替换同样数目的鸡来减少脚数，每去掉一只兔（换进一只鸡）减少2只脚，需要去掉多少只兔（即换进多少鸡）才能减少46只脚？显然

有鸡46÷2=23（只）

有兔35-23=12（只）

若用数学综合式计算为：

有鸡（35×4-94）÷（4-2）=23（只）

有兔35-23=12（只）

答：鸡23只，兔12只。

当然，此题还有别的解法，欢迎数学小能手们补充。

三

三藏西天去取经，

一去十万八千程。

每日常行七十五，

问公几日得回程。

——梅瑴成《增删算法统宗》

【译文】唐朝的三藏前往佛教***去取经，走了108000里，每天平均走75里，试问唐僧一行多少日后返回来？

【解法】

108000÷75=1440（日）

所以到达西天需要1440÷360=4（年）

来回时间为2×4=8（年）

答：唐三藏取经1440日即4年后到达西天，8年后回来，忒简单！

四

百兔纵横走入营，

几多男女斗来争。

一人一个难拿尽，

四只三人始得停。

来往聚，闹纵横，

各人捉得往家行。

英贤如果能明算，

多少人家甚法评。

——梅瑴成《增删算法统宗》

如果说，上面几题字面意思还稍微能看懂，这题就有点考验理科生了。现在来翻译下：

有100只野兔，从四面八方跑进山野村寨，男男女女都来争捉兔子。这批兔子若1人得1只有余；若4只兔子分给3个人，则恰好分尽。围捉兔子的男女十分欢喜，高兴地喊叫着。只见每人拿着捉得的兔子往家走。聪明的人快来算一算，捉兔的男女共有多少人？

此词题若用纯数学表达：“100只兔子，1人分1只有余，3人分4只正好分尽，问有多少人？”

【解法一】若将4只兔子分为一组，则100只兔子共有100÷4=25（组），由于一组兔分给3个人，因此，25组应有25×3=75（人）。

答：共有75人。

【解法二】（古算书解法）根据题意列出综合式：

100÷4×3=75（人）

看完是不是有点想用小锤锤敲打作者的胸口？看起来如此拗口的诗词，翻译了半天，原来是这么道“眼熟”的小升初的数学题！

五

一求隔位六二五，

二求退位一二五，

三求一八七五记，

四求改曰二十五，

五求三一二五是，

六求两价三七五，

七求四三七五置，

八求转身变作五。

——杨辉《日用算法》

看完这首诗，是不是觉得上面那道题根本不算啥？

还是辛苦小编翻译一下好了。

【译文】1两化为0.0625斤，2两化为0.125斤，

3两化为0.1875斤，4两化为0.25斤，

5两化为0.3125斤，6两化为0.375斤，

7两化为0.4325斤，8两化为0.5斤（旧制八两为半斤）。

【解法】根据古制1斤=16两，则

1两=1÷16=0.0625（斤）

2两=2÷16=0.125（斤）

3两=3÷16=0.1875（斤）

4两=4÷16=0.25（斤）

5两=5÷16=0.3125（斤）

6两=6÷16=0.375（斤）

7两=7÷16=0.4375（斤）

8两=8÷16=0.5（斤）

【探源】这是南宋数学家杨辉为了人们快速将两化为斤的歌诀，记载在他写的《日用算法》（1262）中。称为“化零歌”。《日用算法》早已散佚，但从保存下来的杨辉自序中有“编诗括十有三首”，这里是其中一首。

之前有网友在网上发文：翻开数学教材，似乎里面只有西方大咖，中国数学家的身影从未出现过，为何？

想必看完了以上五个案例，你应该早得出答案了：因为中国古代的数学家，***后都变成了文学家！