立体图形有哪些？小学阶段常见的几种立体图形

小学阶段起初接触到的比如：三角形、长方形、正方形、圆等这些属于在一个平面内的平面图形。

但立体图形就不一样了，它是由多个面组成。以正方形与正方体为例。正方形只有一个面，而正方体有六个面，即：上面、底面、左面、右面、前面和后面。正方体是有高度的，而正方形没有。

根据规则的立体图形的对称性，一般采用三视图法来观察，比如求堆积体的表面积，一般会根据三视图所看到的面乘以2。

说到立体图形有柱体与锥体之分。说通俗一点，上下一样粗，上下有两个完全一样的面，且顶点数也相等的叫做柱体。比如说圆术、四棱柱、三棱柱。

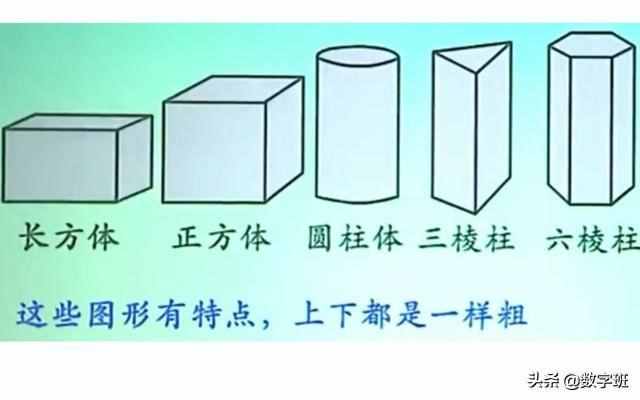
柱体

锥体就不同了，整个图形上下不一样“粗”，只有一个底面，顶上变成了一个点。比如说圆锥、三棱锥以及四棱锥，他们都有个特点，顶部是尖尖的。

我们分别看看一些常见的立体图形，如果沿着棱剪开之后会是什么样子。

以***常见的正方体为例，一个正方体，有6个面，12条棱，而且每条棱的长度是一样的。如果将正方体沿着它的棱剪开，但是不要剪断，大家会发现正方体它的展开图形式有多达11种。反过来说如下图所示的11种图形也能折成正方体。

正方体展开图多达11种

其中“141”这种形式的展开图就有6种。“231”情形的有3种；“222”的只有1种，“33”形状有1种。

能折成正方体的情形太多，需要一定的空间想象力，不容易记住。那么我们反过来记住怎么判断一个图形不能折成正方体？

在展开图上绝对不能出现有“田字格”。一旦有田字格是不能够折成正方体的；另外如果出现“凹”字形，这样的图形沿着折痕也是无法构成正方体的。

点动成线，而线动成面，面动成体。从立体图中我们可以看到哪些平面图形？我们以几种常见的立体图形为例。

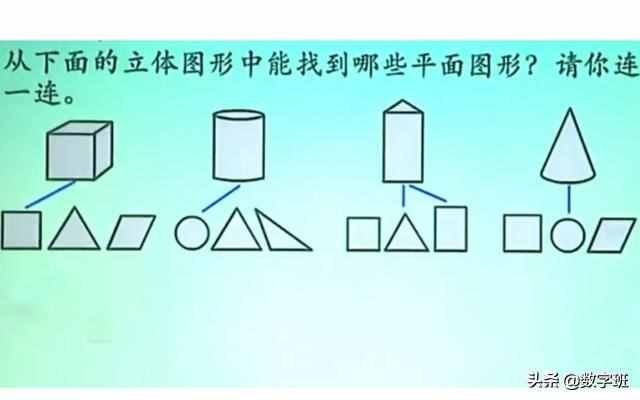
能看到什么平面图形

上图中正方体每个面都一样，只能看到正方形。第2个图形是圆柱，那我们所能看到的就是圆，第3个图形是三棱柱，那我们能看到什么呢？从正面我们可以看到一个长方形，如果从上面看，也就是我们平常说的俯视图看是一个三角形，所以说这个图形我们可以看到，三角形和长方形，这两种平面图形，这个比较特殊一点。那么圆锥呢？圆锥看到的是一个圆。

我们看一下这些图中，找出不同类的。

找出不同的立体图形

***组图形当中，几乎都是圆柱体，所有的柱体求体积都可以用底面积乘以高这个公式。显然有一个是不一样的，倒数第二个它是一个圆台。

第二组图形中，哪个不一样呢？不好确定的话可以用排除法。有一点需要注意的是，球体是可以滚动的，圆是平面图形，它不能滚动。

第三组立体图形中，有一个是三棱柱，其他的都是椎体，所以说三棱柱与其他不同类。

下图中是常见的几种立体图形的展开图。

请将展开图片与立体图连一连

其中右上角的那个很漂亮也很奇怪，可能一眼看不出来，不过用排除法选定其他立体图形后，会发现它是四棱锥的展开图。